本文主要讲解诸如时间、空间、算法等的复杂度表达方式。
相信很多人第一眼看到O(1)、O(n)、O(logn)、O(nlogn) 、O(n^k)会一脸蒙蔽,这些常用来表示时间、空间、算法等的复杂程度。这些是按数量级递增排序,常见的有常数阶O(1)、线性阶O(n)、对数阶O(log2n)(以2为底n的对数,不清楚的回去复习对数函数相关知识,下同)、线性对数阶O(nlog2n)、平方阶O(n^2)、立方阶O(n^3)、k次方阶O(n^k)、指数阶O(2^n),随着问题规模n的不断增大,上述复杂度不断增大,执行效率越低。
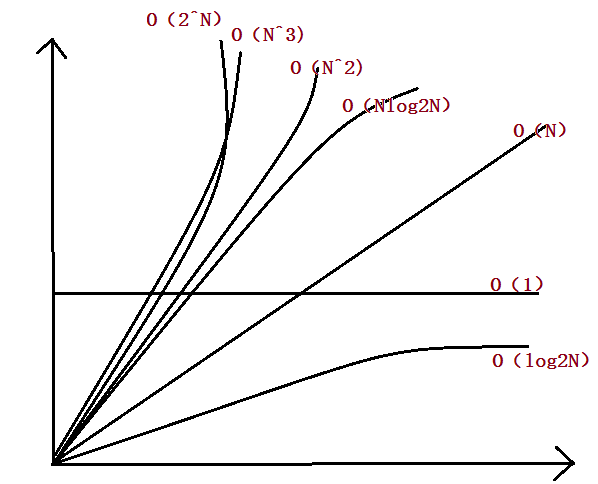
关于表达方式大O加上()的形式,里面是一个函数f()即O(f()),指明复杂度的耗时/耗空间/耗资源与数据增长量之间的关系,其中的n代表输入数据的量。关于为什么要用大O,这个涉及到渐近记号(Asymptotic Notation)的大O符号(Big O Notation)。
这里简单说一下大O符号(Big O notation),是用于描述函数渐进行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。
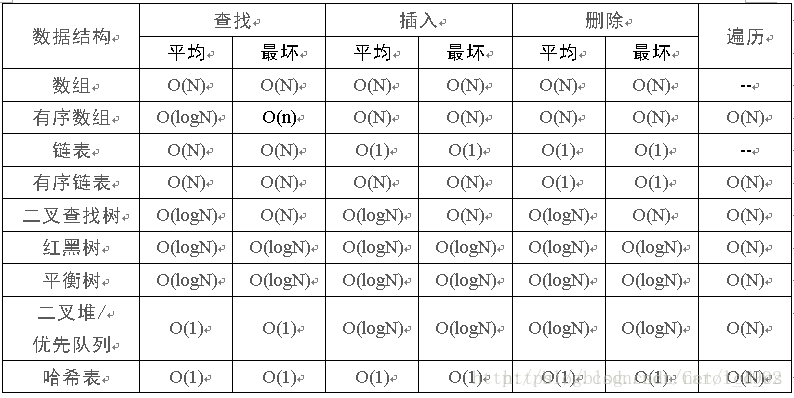
| 复杂度 | 标记符号 | 描述 |
| 常量(Constant) | O(1) | 操作的数量为常数,与输入的数据的规模无关。n = 1,000,000 -> 1-2 operations |
| 对数(Logarithmic) | O(log2 n) | 操作的数量与输入数据的规模 n 的比例是 log2 (n)。n = 1,000,000 -> 30 operations |
| 线性(Linear) | O(n) | 操作的数量与输入数据的规模 n 成正比。n = 10,000 -> 5000 operations |
| 平方(Quadratic) | O(n2) | 操作的数量与输入数据的规模 n 的比例为二次平方。n = 500 -> 250,000 operations |
| 立方(Cubic) | O(n3) | 操作的数量与输入数据的规模 n 的比例为三次方。n = 200 -> 8,000,000 operations |
| 指数(Exponential) | O(2n) O(kn) O(n!) | 指数级的操作,快速的增长。n = 20 -> 1048576 operations |
注1:快速的数学回忆,logab = y 其实就是 ay = b。所以,log24 = 2,因为 22 = 4。同样 log28 = 3,因为 23 = 8。我们说,log2n 的增长速度要慢于 n,因为当 n = 8 时,log2n = 3。
注2:通常将以 10 为底的对数叫做常用对数。为了简便,N 的常用对数 log10 N 简写做 lg N,例如 log10 5 记做 lg 5。
注3:通常将以无理数 e 为底的对数叫做自然对数。为了方便,N 的自然对数 loge N 简写做 ln N,例如 loge 3 记做 ln 3。
注4:在算法导论中,采用记号 lg n = log2 n ,也就是以 2 为底的对数。改变一个对数的底只是把对数的值改变了一个常数倍,所以当不在意这些常数因子时,我们将经常采用 “lg n”记号,就像使用 O 记号一样。计算机工作者常常认为对数的底取 2 最自然,因为很多算法和数据结构都涉及到对问题进行二分。
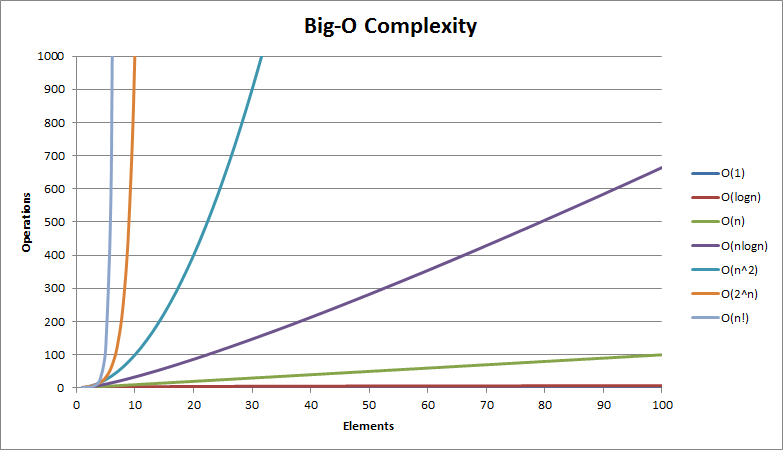
而通常时间复杂度与运行时间有一些常见的比例关系:
| 复杂度 | 10 | 20 | 50 | 100 | 1000 | 10000 | 100000 |
| O(1) | <1s | <1s | <1s | <1s | <1s | <1s | <1s |
| O(log2(n)) | <1s | <1s | <1s | <1s | <1s | <1s | <1s |
| O(n) | <1s | <1s | <1s | <1s | <1s | <1s | <1s |
| O(n*log2(n)) | <1s | <1s | <1s | <1s | <1s | <1s | <1s |
| O(n2) | <1s | <1s | <1s | <1s | <1s | 2s | 3-4 min |
| O(n3) | <1s | <1s | <1s | <1s | 20s | 5 hours | 231 days |
| O(2n) | <1s | <1s | 260 days | hangs | hangs | hangs | hangs |
| O(n!) | <1s | hangs | hangs | hangs | hangs | hangs | hangs |
| O(nn) | 3-4 min | hangs | hangs | hangs | hangs | hangs | hangs |
计算代码块的渐进运行时间的方法有如下步骤:
- 确定决定算法运行时间的组成步骤。
- 找到执行该步骤的代码,标记为 1。
- 查看标记为 1 的代码的下一行代码。如果下一行代码是一个循环,则将标记 1 修改为 1 倍于循环的次数 1 * n。如果包含多个嵌套的循环,则将继续计算倍数,例如 1 * n * m。
- 找到标记到的最大的值,就是运行时间的最大值,即算法复杂度描述的上界。
参考:
https://blog.csdn.net/ted_cs/article/details/82881831
https://blog.csdn.net/lhq186/article/details/88031799
https://blog.csdn.net/ffsiwei/article/details/80424275
https://baike.baidu.com/item/%E5%A4%A7O%E7%AC%A6%E5%8F%B7/656100
展开阅读全文
上一篇: Mac上卸载Java(JDK)


 扫码打开小程序可评论文章保存图片,在“我的”有实时在线客服哦,
扫码打开小程序可评论文章保存图片,在“我的”有实时在线客服哦,
 关注我的公众号为您分享各类有用信息
关注我的公众号为您分享各类有用信息 分享录多端跨平台系统
分享录多端跨平台系统 粤公网安备 44011202001306号
粤公网安备 44011202001306号